2025. 1. 18. 15:59ㆍProgrammers
● 문제 설명


●문제 요약
1. 주어진 전체 시간(limit) 내에 모든 퍼즐을 해결하기 위한 최소한의 숙련도(limit)를 구해야함.
2. 퍼즐이 4단계로 구성되어있고 level이 2이고, 주어진시간(limit)가 59이고, 난이도는 각각 [1,4,4,2] 이고, 각 난이도에 걸리는 시간이 [6,3,8,2]일 경우
[1번째 퍼즐에 걸리는 시간 = 2]
[2번째 퍼즐에 걸리는 시간 = (4-2)번 틀려서 총 (3+6)x2+3 = 21]
[3번째 퍼즐에 걸리는 시간 = (4-2)번 틀려서 총 (8+3)x2+8 = 30]
[4번째 퍼즐에 걸리는 시간 = 2]
총 2+21+30+2 = 59라는 시간을 사용하여 퍼즐을 해결, 만약 level이 2보다 낮을 경우 59보다 시간이 더 걸리기 때문에 2를 return 해야함.
●문제 풀이
제한 사항을 보면 diffs의 길이가 100000이 나올수도 있기 때문에 for문을 사용하여 level을 1씩올려서 비교하는 방법은 자제해야한다. (시간이 엄청 걸리기 때문)
그러면 어떻게 이 문제를 풀어야할까?

위의 그림을 설명하면, 각 숙련도에 따른 결과를 나타낸 그림이다. 만약 나의 숙련도(level)이 6일 경우는 제한 시간(limit)내에 퍼즐을 맞추지 못하지만 나의 숙련도(level)가 7일 경우는 제한 시간(limit)내에 퍼즐을 맞출 수 있는 최소 숙련도이기 때문에 7을 return해야한다. 이 실패와 성공의 경계선을 빠른 속도로 찾아야 하는 것이 관건이다.
이런 문제를 해결할 때 level을 1씩올려서 하기보단 level을 더 큰 폭으로 올려서 해결해야 더 빠르지 않을까? 그럴 때 쓰는 알고리즘이 이분 탐색이다.
이분탐색이란 데이터의 중간 값을 확인하여 목표 값과 비교하는 방식이다. 이 방식은 한 번 탐색할 때마다 탐색 범위를 절반으로 줄이므로 시간복잡도가 O(log n)이다.

만약 현재 level에서 실패할 경우 성공할 경우 level을 낮춰야하기 때문에 그 기준점이 되는 prev_level을 현재 level로 바꾸고 level을 현재 level과 end의 중간으로 설정하여 큰 폭으로 level을 상승시킨다..

현재 level에서 성공할 경우 level을 낮춰야하므로 기준점이 되는 prev_level과 현재 level사이로 level을 조정한다. 그와 동시에 실패할 경우 end도 현재 level로 설정해준다.(위의 그림처럼 level이 3에서 실패할텐데 다시 level을 3과 10사이에서 조정하기보단 최근에까지 성공한 5랑 3사이에서 조정하는 것이 훨씬 효율적이기 때문)

값을 return할 때는 위와 같은 규칙을 가지면 level을 return해준다. 위의 첫 번째 그림에서 prev_level 바로 뒤에 level이 있고 해당 level에서 성공할 경우 그 곳이 경계이기 때문에 해당 level을 return한다.
두 번째로 level을 조정하면서 prev_level과 level이 동일한 경우가 있다. (level을 조정하는데 홀수/2가 되어서 소수점이 나와버리면 내림이 되기 때문 ex) 6+7 = 13 / 2 = 6.5 = 6) 그런 불상사가 일어날 때를 대비해서 위와 같은 상황이 일어날 경우 해당 end를 return 해준다.

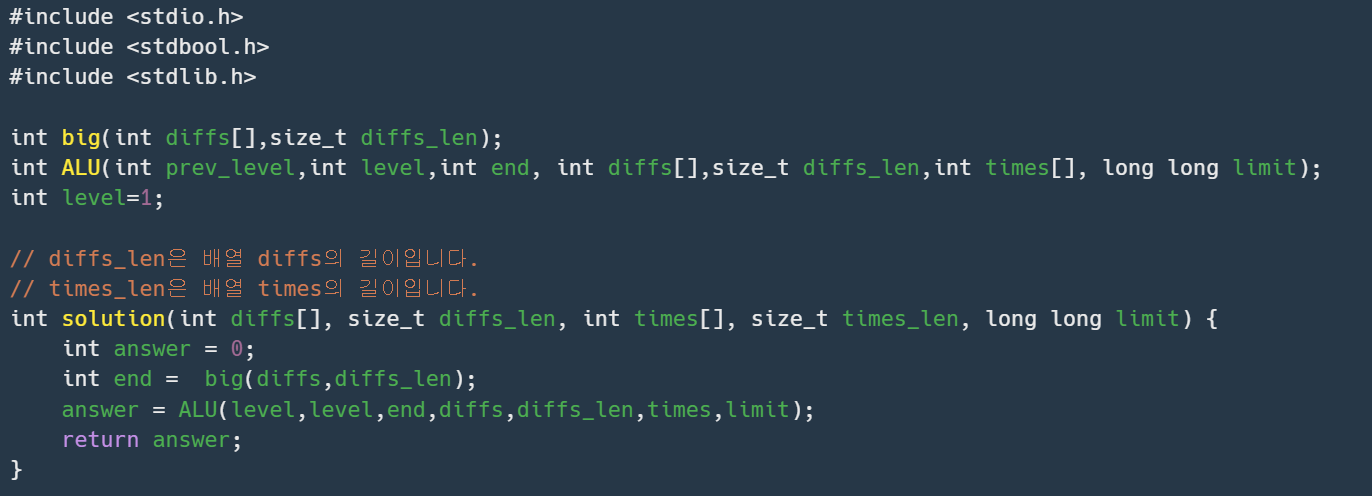
먼저 end를 구해준다. end는 퍼즐 난이도 중에 가장 높은 난이도를 의미한다.

위에서 설명한 방식대로 동작하는 코드이다.
total_time은 모든 퍼즐을 푸는 데 걸리는 시간, plus_time은 만약 자신의 숙련도보다 퍼즐의 난이도가 높을 경우 추가로 걸리는 시간이다.
success부분에서 처음 if(level==1) return level 부분은 자신의 숙련도가 1인데도 성공하면 모든 숙련도에서 성공할 것이기 때문에 1을 반환한다.
perfect success는 특정 숙련도에서 모든 퍼즐을 제한 시간에 딱 맞춰서 해결하면 그 숙련도가 경계이기 때문에 해당 숙련도를 반환한다.
'Programmers' 카테고리의 다른 글
| [PCCP 기출문제] 1번 / 동영상 재생기 (0) | 2025.01.16 |
|---|---|
| 덧칠하기 (1) | 2024.09.03 |
| 대충 만든 자판 (0) | 2024.08.18 |
| 햄버거 만들기 (0) | 2024.08.04 |
| 뒤에 있는 큰 수 찾기 (0) | 2024.07.19 |